기본
선형회귀분석과 유사하지만 종속변수가 양적척도가 아닌 질적척도라는 차이가 있음. 즉, 로지스틱 회귀분석은 특정 수치를 예측히는 것이 아니라 어떤 카테고리에 들어갈지 분류를 히는 모델. 기본 모형은 종속변수가 0과 1이라는 이항(binary)으로 이루어져 구매/미구매, 성공/실패, 합격/불합격 등을 예측한다.

선형 회귀선은 이항으로 이루어진 종속변수를 직선으로 표현하려다 보니 확률이 양과 음의 무한대로 뻗어 나가버린다. 이러한 방식은 확률을 표현하기에 적합하지 않기 때문에 그림 13.6의 오른쪽 형태와 같이 0과 1 사이의 S자 곡선의 형태를 갖도록 변환해 줘야 한다. 즉, 종속변수의 값을 1이 될 확률이라 정의하고 값이 0.5보다 크변 1, 작으면 0으로 분류하는 것이다. 물론 분류하는 기준값은 상황에 따라 달라질 수 있다.
시그모이드 함수
로지스틱 회귀분석에서는 종속변수가 0 또는 1이기 때문에 을 이용해서 예측하는 것은 의미가 없다. 그래서 를 이용하는데 는 다음과 같이 정의 된다. 확률 가 주어져 있을 때

로 정의한다.
odds는 특정 사건이 일어날 확률과 일어나지 않을 확률의 비율을 의미한다. 예를 들어, 어떤 경기에서 A 선수가 이길 확률이 1/3이라면, A 선수가 이길 odds는 1:2가 된다. 이와 같이 odds는 일어날 확률과 일어나지 않을 확률의 비율을 나타내므로, 이를 로그 변환하여 사용하면 선형적인 값을 얻을 수 있다. 따라서, 이를 활용하여 로지스틱 회귀 모델에서는 입력값과 가중치의 곱에 대한 로그 오즈 비율을 예측하고, 이를 시그모이드 함수에 입력하여 0과 1 사이의 확률 값을 구하게 된다.

결과해석 방법
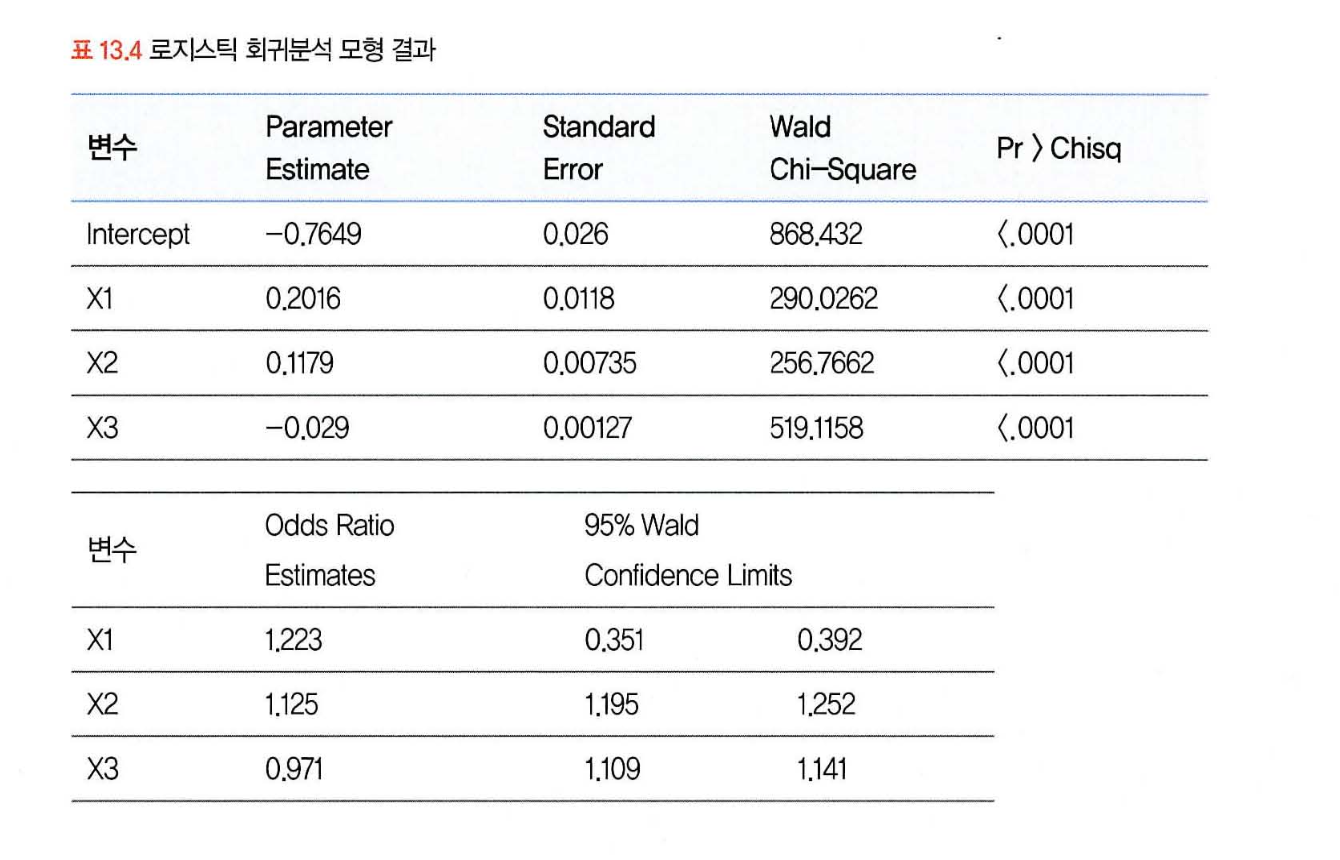
X1은 1이 커질 때마다 1일 때 0에 비해 종속변수가 1.223배로 1일 확률이 높다는 것.
*로지스틱 회귀분석은 결정계수를 구하는 대표적인 방법은 없다. 공식적으로 알려진 방법만 10가지가 넘는다.
*ROC Curve, Confusion matrix 등 다양한 적합도 판단 기준 존재
실습
'Data Science > Regression Analysis' 카테고리의 다른 글
| 회귀 모델의 성능 평가 지표 (0) | 2023.11.16 |
|---|---|
| Decision Tree and Random Forest (0) | 2023.04.02 |
| Linear Regression Analysis & Elastic Net (0) | 2023.04.02 |
