회귀분석의 원리
회귀분석은 해당 객체가 소속된 집단의 x(독립변수) 평균값을 통해 y(종속변수) 값을 예측히는 것이 기본적인 원리다.
회귀 분석을 한마디로 정의하면, “종속변수 Y의 값에 영향을 주는 독립변수 X들의 조건을 고려하여 구한 평균값”이라할수 있다.

회귀분석은 오차항을 최소화하는 절편과 기울기를 구하는 것.
y : 예측하고자 하는 값
b_0 : 절편
b_1 ~ b_n : 각 독립편수가 종속변수에 주는 영향력(계수)값
e: 잔차(모델에 의해 설명되지 않는 부분)

Least Square Method (최소제곱추정법)
최적의 회귀선을 구하기 위해선, 회귀선과 각 관측치를 뜻하는 점 간의 거리를 최소화히는 것이다. 예측치와 관측치들 간의 수직 거리(오차)의 제곱합을 최소로 하는직선 이 회귀선이 된다.
선형회귀분석의 기본가정
(1) 정규성 : 잔차가 평균이 0인 정규분포를 띈다.
(2) 독립성 : 잔차 사이에는 상관관계가 없이 독립이어야 한다.
(3) 등분산성 : 잔차의 분산은 입력변수와 무관하게 일정해야 한다.
(4) 선형성 : 입력변수와 출력변수 사이에는 선형적인 관계를 띄어야 한다.
+ 다중회귀분석을 진행할 때는 독립 변수 간에 다중공선성이 없어야함 - > VIF,상관분석 등을 통해 확인
다항 회귀(Polynomial regression)
다항회귀란 독립변수와 종속변수의 관계가 비선형 관계일 때 변수에 각 특성의 제곱을 추가하여 회귀선을 바선형으로 변환하는 모텔

* 다항회귀는 차수가 커질수록 편향은 감소하지만 변동성이 증가하게 됨 -> 분산이 늘어나고 과적합 유발.
회귀분석 기본 가설 및 결과 해석
귀무가설: 모든 회귀계수가 0이다.
대립가설: 적어도 하나의 변수는 회귀계수가 0이 아니다

Parameter Estimate(계수) : X1의 계수가 0.604라는 것은, 독립변수 X1의 값이 1씩 커질 때마다 종속 변수 Y값이 0.604만 큼 커진다는 것을 의미
Intercept(절편) : 종속변수의 기본값은 24.822로 시작하여 각 독립변수들의 값 x계수 조합으로 종속변수의 값이 예측됨.
Standard Error(표준오차) : 해당 값이 크다는 것은 그만큼 예측값과 실젯값의 차이가 크다는 것을 의미 /
T-Value : 노이즈 대비 시그널의 강도/ 독립변수와 종속변수 간에 선형관계가 얼마나 강한지를나타내기 때문에, 값이 커야 함 / 하지만 일일이 보기에는 비효율적이기 때문에 P-value를 사용
P-value : 일반적으로 0.05 이하의 값인 경우에 95% 귀무가설 기각역에 포함하므로 해당 변수가 유의하다고 판단
Tolerance, VI : Tolerance의 역수가 VIF값이기때문에 하나만 봐도 무관
변수 선택
전진 선택법(Forward Selection): 가장 단순한 변수선택법으로, 절편(Intercept)만 있는 모델에서 시작하여 유의미한 독립변수 순으로 변수를 차례로 하나씩 추가하는 방법
후진 제거법 (Backward Elimination): 모든 독립변수가 포함된 상태에서 시작하여 유의미하지 않는 순으로 설명변수를하나씩 제거하는방법이
단계적 선택법 (Stepwise Selection): 전진 선택법과 후진 제거법의 장점을 더한 방법이다. 처음에는 전진선택법과 같이 변수를 하나씩 추가하기 시작하면서 선택된 변수가 3개 이상이 되면 변수 추가와 제거를 번갈아 가며 수행 / 오래걸림
Ridge와 Lasso & Elastic Net
Ridge(L2-norm): 전체 변수를 모두 유지하면서 각 변수의 계수 크기를 조정하는 방법. 종속변수 예측에 영향을 거의 미치지 않는 변수는 0에 가까운 가중치를 주게 하여 독립변수들의 영향력을 조정해 주는 것이다. 이러한 조정을 계수 정규화Regularization)라 한다. 이를 통해 다중공선성을 방지하면서 모델의 설명력 최대화 가능.
Lasso(L1-norm): Ridge와 유사하지만, 중요한 몇 개의 변수만 선택하고 나머지 변수들은 계수를 0으로 주어 변수의 영향력을 아예 없앤다는 차이가 있다. Lasso는 파라미터 값의 크기에 상관없이 같은 수준으로 정규화를 하기 때문에 영향력이 작은 변수를 모델에서 삭제한다. 따라서 모델을 단순하게 만들 수 있고 해석이 용이하다.
Elastic Net: Ridge와 Lasso의 최적화 지점이 다르기 때문에 두 정규화 항을 결합하여 절충한 모델. Ridge는 변환된 계수가 0이 될 수 없지만 Lasso는 0이 될 수 있다는 특성을 결합.이러한 혼합비율(r)을 조합하여 성능을 최적으로 이끌어 냄. r이 0에 가까울수록 Ridge와 같아지며, 1에 가까울수록 Lasso와 같아짐.
다중 회귀분석 모형 결과 해석
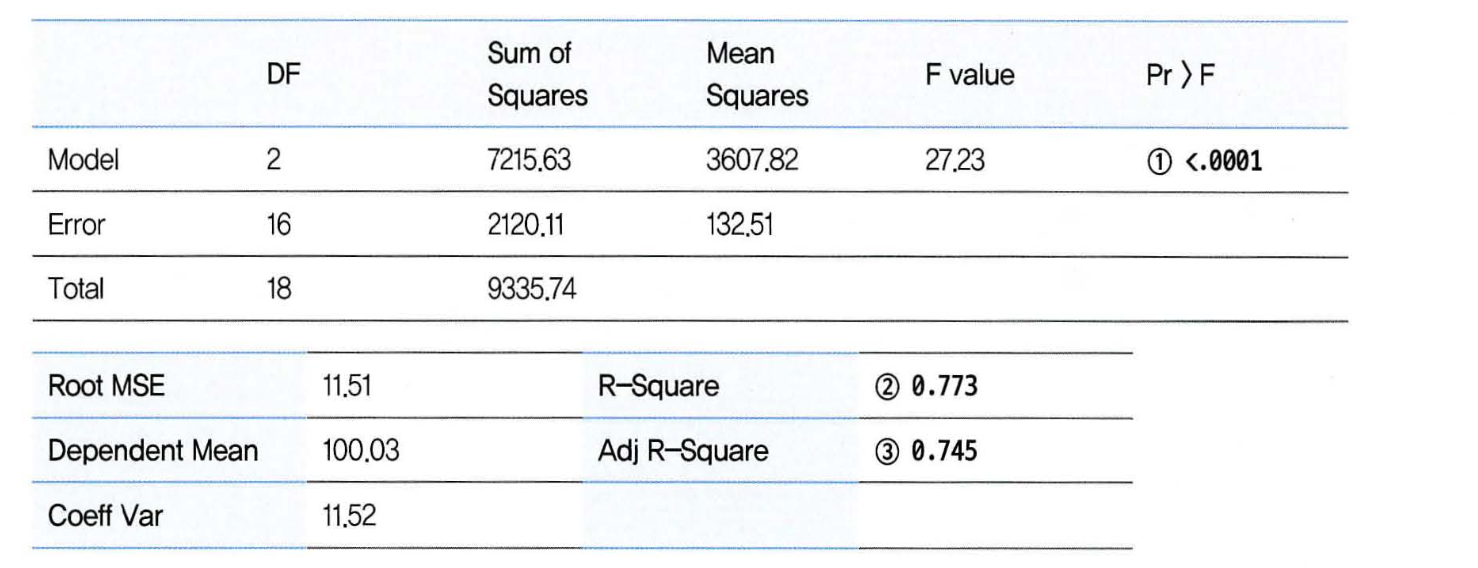
1번 : 적어도 한 개 이상의 독립변수는 회귀계수가 0이 아니다.
2번 : 결정계수(설명력), 어느정도 설명할 수 있는지.
사용된 변수가 많을 경우에는 3번을 함께 보고 설명력 판단 요함.
실습
'Data Science > Regression Analysis' 카테고리의 다른 글
| 회귀 모델의 성능 평가 지표 (0) | 2023.11.16 |
|---|---|
| Decision Tree and Random Forest (0) | 2023.04.02 |
| Logistic regression (0) | 2023.04.02 |
