시계열 데이터의 속성
시계열(종단면) 데이터 vs 비시계열(횡단면) 데이터
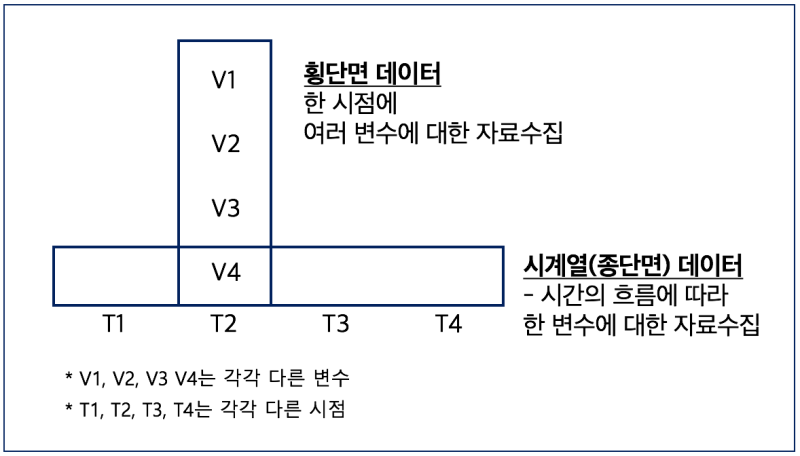
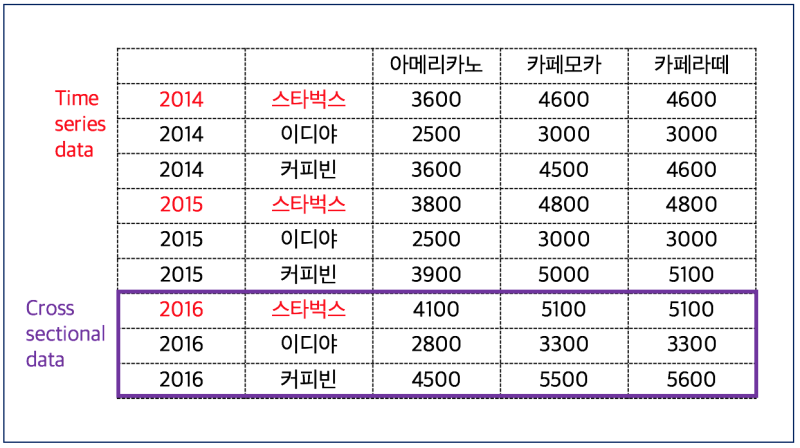
시계열 데이터의 특징
- 계절성(s)
- 추세성(t)
- 반복성(r)
- 순환성(c)
- 자기상관성(Autocorrelation): 횡단면 데이터의 가정 (i.i.d.) = individually and independently distributed, 각 데이터 포인트는 각각 독립
- 정상성(定常, stationarity)
- 단위근(Unit Root) 존재여부 검정
- KPSS(Kwiatkowski-Phillips-Schmidt-Shin Test) 검정: (H0) 단위근이 존재하지 않을 것이다
- ADF(Augemented Dickey-Fullter Test) 검정: (H0) 단위근이 존재할 것이다
- 등분산성(or 이분산성, Heteroskedasticity)
다양한 형태의 시계열 데이터
- 우연변동
- 계절변동
- 추세변동
- 계절적 추세변동
- 순환변동
시계열 데이터 처리
- 빈도(f) 추가
- 차분
- lag 처리 등
시계열 분석 모형 개요
데이터 가정에 따른 시계열 모형
- 시계열 자료는 추세변동, 계절변동 등 크고 작은 다양한 변동요인이 다중적으로 중첩되어 있다.
- 이러한 시계열 데이터의 분석을 수행할 때는 크게 2가지 접근으로 나눌 수 있다.
- 내포된 변동요인이 고정적 패턴을 보이는 경우: 요소분해법
- 다양한 변동요인이 고정적 패턴을 보이지 않는 경우: (지수)평활법
- 분석모형에 따라 추정된 추정값과 관측값과의 차이인 잔차의 시계열 자료(Residual Error Series)는 확률과정으로 나타낼 수 있다.
- 이때 고려되는 것이 확률모형(Stochastic Model)이다.
- 시계열 분석에서 모형이 잘 적합될 때 잔차의 시계열 자료는 백색잡음(white noise)이 된다
- x_t = y_t - ^y_t =~ N(0, σ^2)
- 즉, 잔차는 서로 독립이다
- 확률모형의 분석은 다음의 4가지 단계를 걸쳐 수행된다
- 모형 설정(Model Identification): ACF, PACF 같은 지표와 auto.arima와 같은 프로그램을 이용하여 시계열 자료에 적합한 모형을 선택
- 모수 추정(Parameter Estimation): 설정한 모형에 따라 모수(계수)를 추정하고 적합성을 검토
- 분석결과의 검정(Statistical Testing): 모형 적합도에 따른 잔차의 정상성 및 분석결과 검정을 수행
- 예측(Forecasting): 시계열 자료와 분석모형을 토대로 미래 값을 예측
- 오차수정 모형: 두 변수간 장기적 관계가 존재할 때 이들 관계를 회귀모형으로 추정하면, 불안정 시계열의 선형결합이 안정적 시계열이 됨
자기상관 함수(Auto Correlation Function, ACF)
- 동일한 변수를 시점을 달리하여 관측했을 때 시점에 따라 다른 값 사이의 상호 연관관계를 나타내는 척도
- 연속적인 관측값 사이의 상호 연관관계
- 시계열 자료에서 time별 signal과 time lag별 signal의 유사성을 토대로 시계열 자료의 정상성 파악
- ACF 그래프는 정상 시계열일 경우 0으로 빠르게 떨어지고, 비정상 시계열은 천천히 떨어진다
부분자기상관 함수(Partial ACF, PACF)
- 산정하고자 하는 연속적인 2개의 시계열 자료에서 상관계수를 구함
- 산정하고자 하는 두 변수를 제외한 모든 변수의 영향을 제거한 상태에서의 두 변수간 존재하는 순수한 상관계수를 산정하여 정상성 검정
- 즉 y_t와 y_t-k 간의 순수한 상관관계
- 두 지점 사이에 포함된 모든 y_t-1, y_t-2, ..., y_t-k+1 의 영향을 제거된다
- 시계열 자료가 정상성인 경우, 자기상관 함수와 부분자기상관 함수 모두 각 시차에서 신뢰한계(일반적으로 표준편차의 2배)의 범위 내에 존재하는 것으로 나타남
자기회귀(AR, Autoregressive Model)
- 변수의 과거 값의 선형 조합을 이용하여 관심 있는 변수를 예측
- 자기 자신에 대한 변수의 회귀
- (선형회귀) y = a + b1 * X_1 + ... + bp * X_p + ε
- (자기회귀) y_t = c + Φ1 * y_t-1 + Φ2 * y_t-2 + ... + Φp * y_t-p + ε_t
- AR(p) : p차 자기회귀 모형
- ε_t 은 평균이 0이고 분산이 1인 정규 분포를 따르는 백색잡음
이동평균(MA)
- 예측 오차를 이용하여 미래를 예측
- MA(q): q차 이동평균 모형
- y_t = c + Θ1 * ε_t-1 + Θ2 * ε_t-2 + ... + Θq * ε_t-q + ε_t
안정 시계열(ARMA)
- p개의 자기 자신의 과거값과 q개의 과거 백색 잡음의 선형 조합
- AR(p) 모형의 정상성, MA(q) 모형의 가역성 조건을 만족해야 함
- ARMA(p, q)
- y_t = AR(p) + MA (q)
- y_t = Φ1 * y_t-1 + Φ2 * y_t−2 + ... + Φp * y_t−p + ϵ_t + Θ1 * ϵ_t−1 + Θ2 * ϵ_t−2 + ... + Θq * ϵ_t−q
- ARMA(1, 0) = AR(1)
- ARMA(0, 1) = MA(1)
- ARMA(1, 1)
불안정 시계열(ARIMA)
- ARIMA(p, d, q) : d차 차분한 데이터에 AR(p) 모형과 MA(q) 모형을 합친 모형
- ARIMA 모형에서 “I” 는 누적(integrated) 을 의미한다
- 이는 비정상(non-stationary) 시계열을 정상(stationary) 시계열로 만들기 위해서 필요한 차분의 횟수를 의미한다
- ARIMA(p, 0, 0) = AR(p)
- ARIMA(0, 0, q) = MA(q)
- p, d, q 값은 AIC, BIC, 그리고 경험적인 자기상관 등 다양한 방법을 통해서 선택할 수 있다
- 자기상관은 ACF 와 PACF 그래프를 그려서 확인한다
- 시계열 데이터가 AR의 특성을 띄는 경우, ACF는 천천히 감소하고 PACF 는 처음 시차를 제외하고 급격히 감소
- 시계열 데이터가 MA의 특성을 띄는 경우, ACF는 급격히 감소하고 PACF는 천천히 감소
'Data Science > Basic study' 카테고리의 다른 글
| 데이터 분석의 기법과 프로세스: CRISP-DM, SEMMA, 그리고 그 응용 (0) | 2025.04.13 |
|---|---|
| 공분산과 상관계수 쉽게 이해하기 - 수식 없이 (1) | 2025.04.07 |
| PCA(주성분분석) 이란 (0) | 2023.09.14 |
| 손실함수(Loss function)과 경사하강법(Gradient Descent) θ 업데이트 풀이 (0) | 2023.08.24 |
| 데이터분석 기초 정리 (0) | 2023.03.04 |
